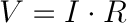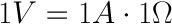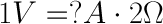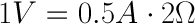Ohm's Law
Electrical Charge
Electricity is the movement of electrons. Electrons create charge, which we can harness to do work. Your lightbulb, your stereo, your phone, etc., are all harnessing the movement of the electrons in order to do work. They all operate using the same basic power source: the movement of electrons.
The three basic principles for this tutorial can be explained using electrons, or more specifically, the charge they create:
- Voltage is the difference in charge between two points.
- Current is the rate at which charge is flowing.
- Resistance is a material’s tendency to resist the flow of charge (current).
So, when we talk about these values, we’re really describing the movement of charge, and thus, the behavior of electrons. A circuit is a closed loop that allows charge to move from one place to another. Components in the circuit allow us to control this charge and use it to do work.
Georg Ohm was a Bavarian scientist who studied electricity. Ohm starts by describing a unit of resistance that is defined by current and voltage. So, let’s start with voltage and go from there.
Voltage
We define voltage as the amount of potential energy between two points on a circuit. One point has more charge than another. This difference in charge between the two points is called voltage. It is measured in volts, which, technically, is the potential energy difference between two points that will impart one joule of energy per coulomb of charge that passes through it (don’t panic if this makes no sense, all will be explained). The unit “volt” is named after the Italian physicist Alessandro Volta who invented what is considered the first chemical battery. Voltage is represented in equations and schematics by the letter “V”.
When describing voltage, current, and resistance, a common analogy is a water tank. In this analogy, charge is represented by the water amount, voltage is represented by the water pressure, and current is represented by the water flow. So for this analogy, remember:
- Water = Charge
- Pressure = Voltage
- Flow = Current
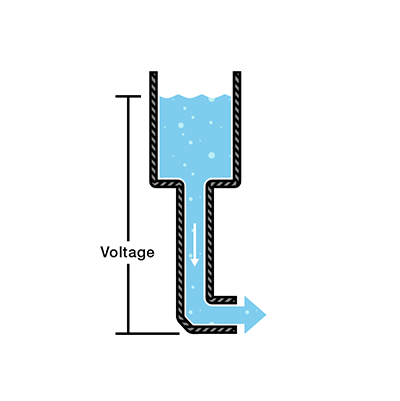
Consider a water tank at a certain height above the ground. At the bottom of this tank there is a hose.
The pressure at the end of the hose can represent voltage. The water in the tank represents charge. The more water in the tank, the higher the charge, the more pressure is measured at the end of the hose.
We can think of this tank as a battery, a place where we store a certain amount of energy and then release it. If we drain our tank a certain amount, the pressure created at the end of the hose goes down. We can think of this as decreasing voltage, like when a flashlight gets dimmer as the batteries run down. There is also a decrease in the amount of water that will flow through the hose. Less pressure means less water is flowing, which brings us to current.
Current
We can think of the amount of water flowing through the hose from the tank as current. The higher the pressure, the higher the flow, and vice-versa. With water, we would measure the volume of the water flowing through the hose over a certain period of time. With electricity, we measure the amount of charge flowing through the circuit over a period of time. Current is measured in Amperes (usually just referred to as “Amps”). An ampere is defined as 6.241*1018electrons (1 Coulomb) per second passing through a point in a circuit. Amps are represented in equations by the letter “I”.
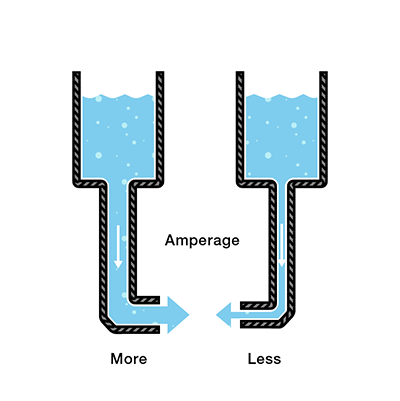
Let’s say now that we have two tanks, each with a hose coming from the bottom. Each tank has the exact same amount of water, but the hose on one tank is narrower than the hose on the other.
We measure the same amount of pressure at the end of either hose, but when the water begins to flow, the flow rate of the water in the tank with the narrower hose will be less than the flow rate of the water in the tank with the wider hose. In electrical terms, the current through the narrower hose is less than the current through the wider hose. If we want the flow to be the same through both hoses, we have to increase the amount of water (charge) in the tank with the narrower hose.
This increases the pressure (voltage) at the end of the narrower hose, pushing more water through the tank. This is analogous to an increase in voltage that causes an increase in current.
Now we’re starting to see the relationship between voltage and current. But there is a third factor to be considered here: the width of the hose. In this analogy, the width of the hose is the resistance. This means we need to add another term to our model:
- Water = Charge (measured in Coulombs)
- Pressure = Voltage (measured in Volts)
- Flow = Current (measured in Amperes, or “Amps” for short)
- Hose Width = Resistance
Resistance
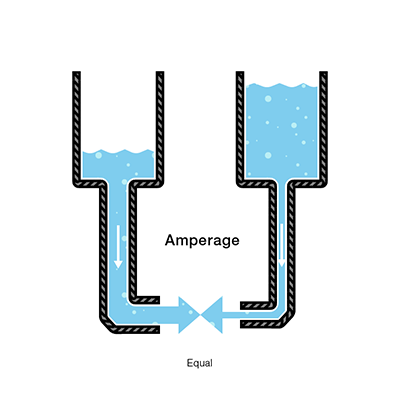
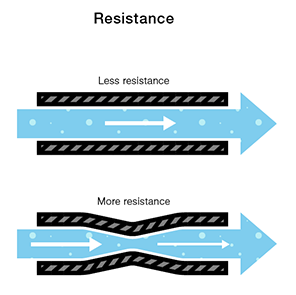
Consider again our two water tanks, one with a narrow pipe and one with a wide pipe.
It stands to reason that we can’t fit as much volume through a narrow pipe than a wider one at the same pressure. This is resistance. The narrow pipe “resists” the flow of water through it even though the water is at the same pressure as the tank with the wider pipe.
In electrical terms, this is represented by two circuits with equal voltages and different resistances. The circuit with the higher resistance will allow less charge to flow, meaning the circuit with higher resistance has less current flowing through it.
This brings us back to Georg Ohm. Ohm defines the unit of resistance of “1 Ohm” as the resistance between two points in a conductor where the application of 1 volt will push 1 ampere, or 6.241×1018 electrons. This value is usually represented in schematics with the greek letter “Ω”, which is called omega, and pronounced “ohm”.
Ohm's Law
Combining the elements of voltage, current, and resistance, Ohm developed the formula:
Where
- V = Voltage in volts
- I = Current in amps
- R = Resistance in ohms
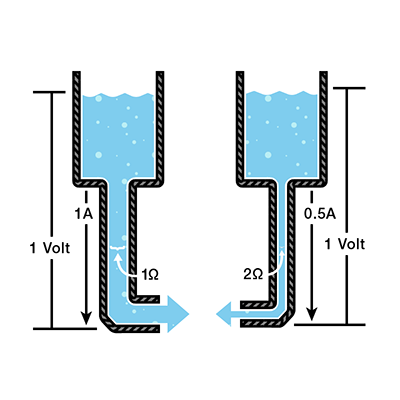
This is called Ohm’s law. Let’s say, for example, that we have a circuit with the potential of 1 volt, a current of 1 amp, and resistance of 1 ohm. Using Ohm’s Law we can say:
Let’s say this represents our tank with a wide hose. The amount of water in the tank is defined as 1 volt and the “narrowness” (resistance to flow) of the hose is defined as 1 ohm. Using Ohms Law, this gives us a flow (current) of 1 amp.
Using this analogy, let’s now look at the tank with the narrow hose. Because the hose is narrower, its resistance to flow is higher. Let’s define this resistance as 2 ohms. The amount of water in the tank is the same as the other tank, so, using Ohm’s Law, our equation for the tank with the narrow hose is
But what is the current? Because the resistance is greater, and the voltage is the same, this gives us a current value of 0.5 amps:
So, the current is lower in the tank with higher resistance. Now we can see that if we know two of the values for Ohm’s law, we can solve for the third.